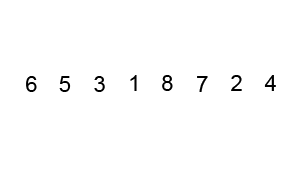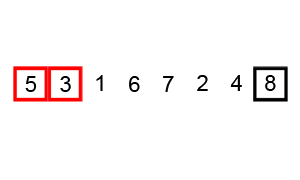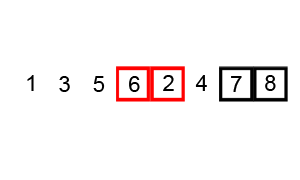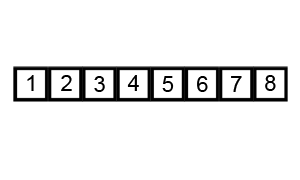Contents

Sorting lists

We saw that sorting lists of data makes searching them more efficient. In this topic, we'll go over some of the ways to sort arbitrary data—strings, ints, chars, your own custom struct and class types, etc. Just as an example, we'll use this short list of numbers when explaining several different sorting algorithms:

5

10

3

20

8

(Back to top)

Bubble sort

Bubble sort is one of the simplest sorts. It's also among the most expensive. For a list of length n, it makes n passes. On each pass, it walks the list from left (index 0) to right, ending at the second-to-last item (index n-2). For each item, it compare the item to its neighbor to the right. So the item at index 0 is compared to the item at index 1. If the one on the left is greater than the one to the right, they are swapped. Then it increments the current index and does the same thing over again until we reach the second to last item. This is one pass. After the first pass, the largest item will have "bubbled" up to the end of the list. We keep making passes until no swaps have been made, which indicates the list is now sorted. In the worst case, we'll have to make n passes. Here's an example using our unsorted array from \ref:

5

10

3

20

8

5

10

3

20

8

5

3

10

20

8

5

3

10

20

8

5

3

10

8

20

Here's what the array will look in the second pass:

5

3

10

8

20

3

5

10

8

20

3

5

10

8

20

3

5

8

10

20

3

5

8

10

20

And here's the third pass:

3

5

10

8

20

3

5

8

10

20

3

5

8

10

20

3

5

8

10

20

3

5

8

10

20

Even though we were actually done sorting after the second pass, we had to do one more to ensure the list was sorted. The third pass is the first time no swaps were made. We would have needed the additional two passes if our data had been sorted in the exact opposite order (the worst case scenario). Here's a look at what happens after each pass if we start with the list backwards (the green boxes are elements that are in their correct sorted position):

20

10

8

5

3

10

8

5

3

20

8

5

3

10

20

5

3

8

10

20

3

5

8

10

20

3

5

8

10

20

Even though it doesn't look like it, we need this last pass to ensure that 3 is in the correct spot. So, in the worst case, we make n passes, each of which makes up to n comparisons. Therefore, our complexity is O(n²).

Wikipedia has a nice animated GIF of the process:

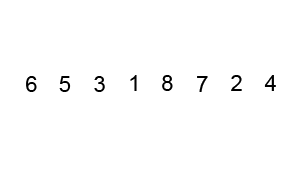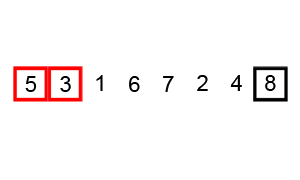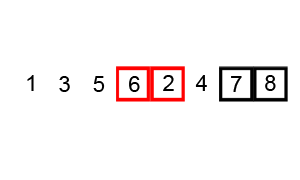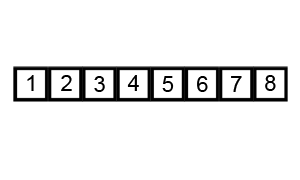
Insertion sort

Insertion sort is another relatively simple algorithm, and indeed has the same worst case complexity as bubble sort: O(n²). With insertion sort, we work our way from the left (index 0) to right (index n-1). The algorithm ensures that everything to the left of the current position is sorted; everything to the right remains to be sorted. At each step, we take the item at the current position and insert it to where it belongs in within the sorted item to the left. In doing this, we need to shift everything from the sorted side that is greater than the current item to the right one position to make room for the item. We then move on to the next unsorted item and continue until we reach the end of the list (all items are to the left).

Wikipedia has a nice animated GIF of the process:

So why is it O(n²)? Because the worst case, when the list is in reverse sorted order, requires that each item be moved to the very left-most spot, causing n comparisons. Since there are n items, we get a complexity of O(n × n) = O(n²).

(Back to top)

Selection sort

Yet another simple sorting algorithm is selection sort, and like the other simple sorting algorithms, has a worst case complexity of O(n²). Selection sort starts with a pointer at index 0. It then walks down the list and finds the minimum item. This is then swapped with the item at the pointer. The pointer is then advanced and we walk from the pointer to the end of the list searching for the minimum. We keep doing this until the pointer has reached the last index, at which point, the list is sorted. Here's the first two passes of our example:

↓
5	10	3	20	8

↓
5	10	3	20	8

↓
3	10	5	20	8

	↓
3	10	5	20	8

	↓
3	10	5	20	8

	↓
3	5	10	20	8

		↓
3	5	10	20	8

We wind up with O(n²) because we have to perform n passes, and we need to perform as many as n comparisons during each pass to find the minimum item, so n × n comparisons.

(Back to top)

Quick sort

Another sort, called quick sort, is, in the worst case, as poor a choice as bubble, insertion, and selection sort. However, in the typical case, quick sort is O(n log₂ n). Here's how it works. First, you pick a pivot item. This can be done at random (to make it easy, just pick the first item). Next, we make two sublists: one with all the items that are smaller than the pivot item, and another with all the larger items. This is called the partition step. Now we do exactly the same process to each of the sublists (it's a multiple recursion algorithm). Once we end up with sublists of one item, we combine them in order, forming a sorted sublist. We begin gluing the sorted smaller items sublist, the pivot, and the sorted sublist of bigger items. We continue to do this until all sublists have been recombined yielding the full sorted list. Here are the steps for our array in \ref. The pivot is the orange box.

5

10

3

20

8

	5
3			10	20	8

	5
3			10	20	8

	5
3			10
		8		20

	5
3			10
		8		20

	5
3		8	10	20

3

5

8

10

20

So, when is this O(n log₂ n)? Provided that we pick "good" pivots for each list/sublist (i.e., ones that will evenly split the list), then we should wind up with log₂ n distinct pivots. That's because we need as many pivots as n can be divided by 2. The n coefficient comes from the fact that each of the n items in the list needs to, in the limit, be compared to each of the pivots. So, we get O(n log₂ n). Now, as we said earlier, this is the average case, not the worst case. In the worst case, we get O(n²). Why? Because if we always choose the worst pivot, i.e., the minimum or maximum for its list/sublist, then we end up with n pivots. That would require a lot of bad luck, but it can happen. So, the worst case is bad, but in practice, this algorithm is usually very...quick.

(Back to top)

Merge sort

Merge sort is another recursive algorithm. However, unlike the previous methods, it runs in O(n log₂ n) in its average and worst case. That's a pretty solid guarantee. So how's it work? Each step of the recursion takes an unsorted list. If the list only has one item in it, it's returned. Otherwise, divide the list in two and sort each half by making a recursive call. Then, merge the resulting sublists. This requires keeping track of two pointers; one pointing to the current item in the one sublist, the other pointing to the current item in the other sublist. The pointers start by pointing at the first item in their respective sublist. Take the smaller item of the two being pointed to and append that to the merged list; advance the corresponding pointer so it points to the next item in that list. Keep doing this until all items have been taken from both sublists. Return the merged list. That's it!

Here's an animated GIF courtesy of Wikipedia:

So why is this O(n log₂ n). The log₂ n comes from the fact that we divide the list in half each time. We can divide a list of length n in half log₂ n times. For each merge step, we perform at most n comparisons. Thus, since there are log₂ n merges, we wind up with a total of n log₂ n comparisons.

While merge sort is faster than quick sort, optimized implementations of quick sort are often used in sorting libraries for programming languages. However, merge sort is found in the libraries of many other programming languages. There is one other sort that is also commonly used, which we will not cover, called heap sort. Heap sort is a variation of selection sort, and depends on a data structure called heap.

(Back to top)

Other sorts

There are many other specialized sorts, e.g., made especially for integers or strings. In addition, there are many data structures that sort data automatically upon insertion. For instance, Binary Search Trees and heaps. For the curious, take a look at the Wikipedia page on sorting algorithms.

(Back to top)