Contents

Trees

A tree is a data structure that looks like an upside down tree. In fact, you've seen trees a lot by now: family trees, organization hierarchies, and really anything hierarchical. A tree that holds numbers is typically represented something like this:

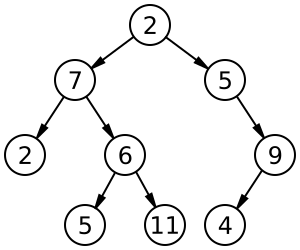
We'll talk more about why trees are an advantageous structure for holding data once we get into binary search trees. Until then, we will just focus on what a tree is.

Trees have several properties. Each circle in \ref is called a node. The top most node in a tree is called the root. A node is connected from above to its parent and below to its children. Nodes that share a parent are called siblings. A node cannot have multiple parents, and as a consequence, a node further down in a tree can never have a node from higher up in the tree as a child. The nodes in a tree above a given node n are referred to as n's ancestors (or antecedents); nodes below are n's descendants. Any node and all of its descendants form a subtree. Nodes without any children are called leaf nodes and all other nodes are called internal nodes. The maximum number of children any node has in tree is called the tree's branching factor. The height of a tree is the number of levels from the root to the farthest leaf. The size of a tree is the total number of nodes, including the root, internal nodes, and leaf nodes.

We can traverse a tree in several ways (i.e., iterate over all the nodes). In a pre-order traversal, we consider the data held by a node first, and then traverse its children. In \ref, a pre-order traversal where we print out the value of each node results in the output: 2, 7, 2, 6, 5, 11, 5, 9, 4. In a post-order traversal, the children of a node are traversed before the data held by the node is. In \ref, a post-order traversal results in the following output: 2, 5, 11, 6, 7, 4, 9, 5, 2.

If a tree is binary (meaning it has a branching factor of two) as the tree in \ref is, then we can also perform an in-order traversal. In this traversal, the left child's subtree is traversed first, followed by the node's data, and then the right child's subtree is traversed. For the tree in \ref, an in-order traversal results in the output: 2, 7, 5, 6, 11, 2, 5, 4, 9. The in-order traversal will make more sense once we talk about binary search trees, where an in-order traversal results in a sorted list of values.

One more note about traversals: they are recursive. For loops are appropriate for lists and arrays, which are linear, but are not a good fit for tree traversals which are non-linear. In a tree, recursion is ideal because we can keep breaking a bigger problem—traversing a tree—into smaller problems—considering a node's data and then traversing its children's subtrees. The base case is reached when we hit the ends of the tree where there are no links to children.

(Back to top)

A Tree as linked nodes

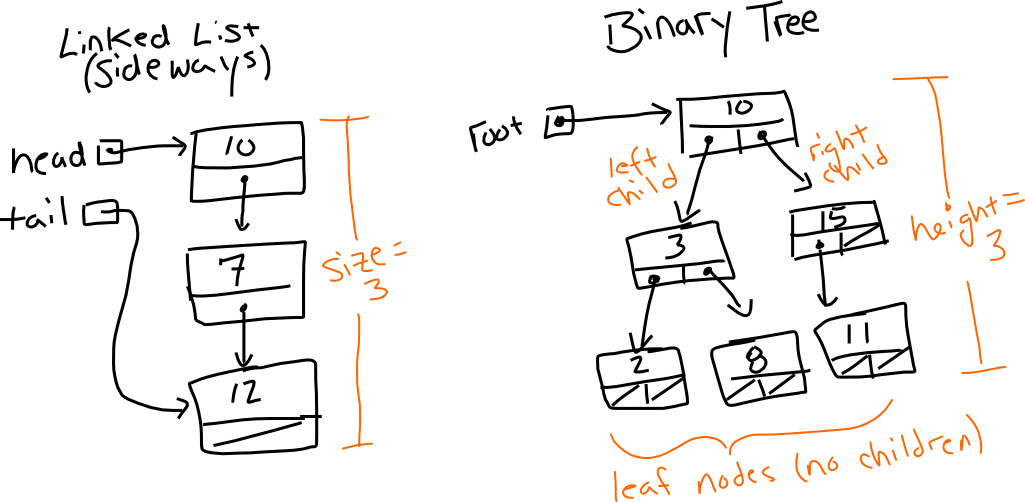
In implementing a tree in code, think about how we programmed linked lists. Linked lists consist of nodes, with each node containing a data value and a pointer to the next node in the list (and, in the case of a doubly linked list, a pointer back to the previous item). We can think of a tree as consisting of very similar nodes, except tree nodes have pointers to their children, of which there can be 0 or more. While we don't show it here, nodes can also have links back to their parent (kind of like doubly linked list). \ref demonstrates how a linked list compares to a binary tree.

Lets consider how we might represent a tree node in C++. First, we will need a data member to hold the value being stored at the node (lets call this data). Second, for a binary tree, we need to store pointers to each of the children, which are called the left and right children (the directions helps when visualizing the tree). We could store these pointers in an array (or list!), but for the special case of binary tree, it's convenient to list these as rightChild and leftChild. Here's what a TreeNode class that stores integers might look like:

Lets represent the binary tree from \ref in C++ using our TreeNode class:

Lets consider one last piece of the implementation: traversal. Specifically, we'll look at how to write a pre-order traversal function for a binary tree using TreeNode that prints the value of each examined node. We will add this traversal directly to the TreeNode interface. Recall that in a pre-order traversal, we print a node's value out before its children.

To perform a pre-order traversal in our example above, we just need to add the statement root->preOrderTraversal();. Now, think about what an in-order traversal would look like in code. What would you expect the output to be?

As one final note, you can actually implement trees using arrays. We will not cover array-based trees in this class, but they do exist.

(Back to top)