Binary Search Trees
Contents
Binary Search Tree ADT
A binary search tree, or BST for short, is an abstract data type that uses a tree with a branching factor of two and arranges data within the tree such that an in-order traversal processes nodes in sorted order. One of the side effects of this is that a BSTs can be easily searched for a target value and, when the BST is balanced (we'll talk about that in a bit), this can be done quickly: O(log2 n).
To meet the constraint that an in-order traversal must process nodes in sorted order, a defining characteristic of a BST is that considering any node x in the tree with a data value d, all the values stored within the nodes of x's left child's subtree must be less than or equal to v, and all the values stored within the nodes of x's right child's subtree must be greater than or equal to v. For example, consider the BST in \ref.
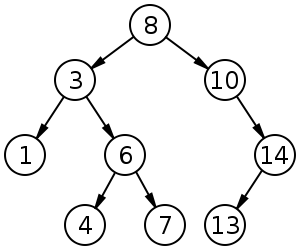
We will consider the following operations for BSTs:
| Operation name | Description |
|---|---|
isEmpty() | Return whether or not the BST is empty |
size() | Return the number of items in the BST |
insert(item) | Adds an item to the tree |
remove(item) | Removes a node matching the item from the tree |
contains(item) | Checks if the tree contains the given item and returns it if it does |
preOrderTraverse(function) | Performs a pre-order traverse of the tree, applying the given function to each node |
postOrderTraverse(function) | Performs a post-order traverse of the tree, applying the given function to each node |
inOrderTraverse(function) | Performs a in-order traverse of the tree, applying the given function to each node |
Understanding the operations
The key to understanding BSTs operations is not in terms of whether they are implemented using linked tree nodes or arrays (though we'll be focusing on the former), but rather understanding the operations on a visualization of the tree. In this section, we'll go through each operation and consider how it works.
isEmpty() and size()
These two are similar to the other ADTs we've seen—size() reports the tree size, which is a data member that is updated any time an item is added or removed from the tree, and isEmpty() reports whether size == 0.
insert(item)
Recall that a key property of BSTs is that for any node in the tree, all the values in the left child's subtree are less than or equal to the value stored at the node, while all the values in the right child's subtree are greater than or equal to the value stored at the node. That means that given a new item, we need to check it against the current node's value v: if the item is less than v, then we insert the item into the left subtree; otherwise, we insert it into the right subtree. Notice that this is the beginning of a recursive solution! Here's what it looks like in pseudo code:
insert(item):
if root doesn't exist (i.e., isEmpty()):
set root to a new node with item as the data
else:
insertHelper(item, root)
insertHelper(item, node):
if item < node's data:
if node has leftChild: insertHelper(item, leftChild)
else: set leftChild to a new node with item as the data
else:
if node has rightChild: insertHelper(item, rightChild)
else: set rightChild to a new node with item as the data
Here's an example of running that code to add the number 8 to a BST. The original tree is on the left, and the tree after the insertion is on the right. The orange nodes are nodes that were examined, and the green node is the one that was created:
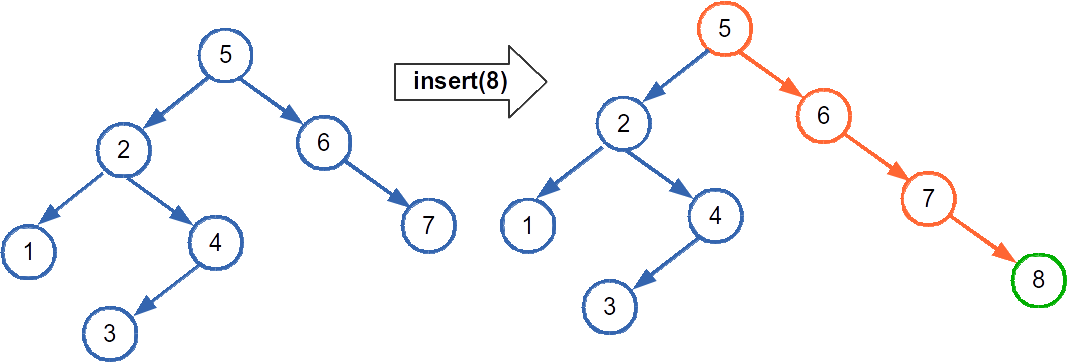
remove(item)
Unlike what we saw with the List, Stack, and Queue ADTs where removing an item involved an explicit or implicit position (e.g., remove(pos) for List), tree's don't have positions or indexes. So, when we want to remove something, we have to specify the data itself. For example, if we have a BST that stores the numbers {5, 6, 10, 15}, and we want to remove the 10, then we need to invoke remove(10). If a BST stores the strings {"Monday", "Tuesday", "Wednesday", "Thursday"} and we want to remove "Wednesday", then we invoke remove("Wednesday").
The remove operation is pretty ugly for BSTs. The main challenge stems from the fact that a node can have up to two children. So if you remove a node from the tree, what do you do with it's children? And don't forget, we have to maintain the property that the left child's subtree must contain values less than or equal to the node, and the right child's subtree must contain values greater than or equal to the node. It turns out there are three special cases when it comes to removing a node:
- the node has no children (it's a leaf)
- the node has exactly one child
- the node has two children
The first case is the easiest to deal with—we just unlink the node from its parent and delete the node. Here's an example of removing the leaf node with the value 7 from a BST:
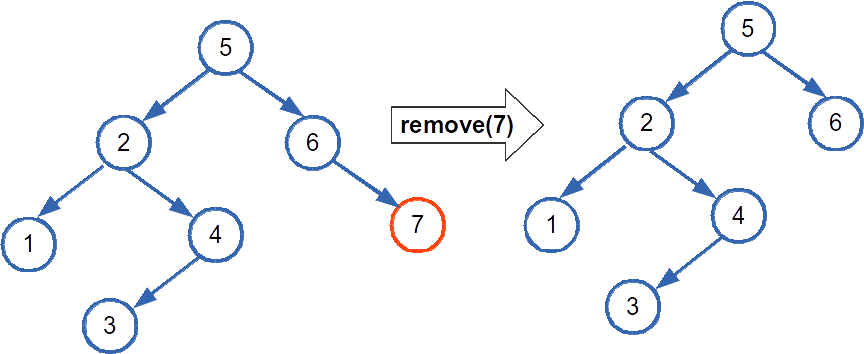
The second case is also pretty easy. We can take the node's only existing child and link it to the node's parent, then delete the node. Heres an example removing a node with the value 4 and a single child. The node with value 3 (whose former location is indicated by the grayed out node) takes the spot that 4 use to hold.
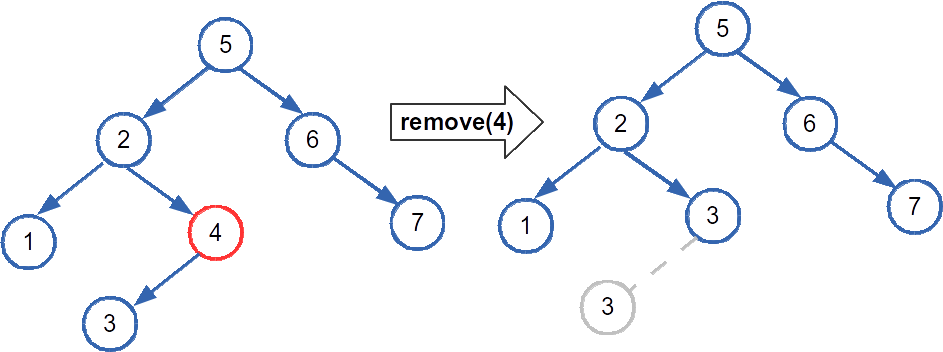
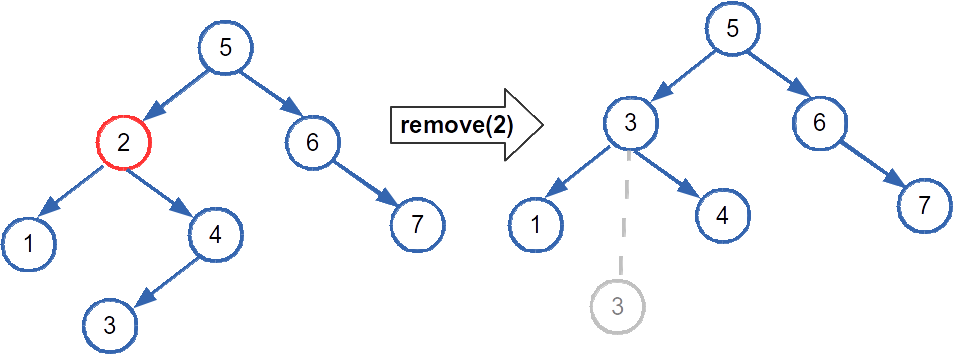
The final case is where the ugly comes in. If both children are present, we cannot link both of them to the node's parent (then the parent would could have three children!). Here's what we do: to remove a node x, unlink the node with the smallest value in x's right subtree and substitute it for x. Then delete x. Here's an example of remove a node, 2, with two children from a BST. The min node from its right subtree, 3, is put in 2's old spot. 3's original location is indicated by the grayed out node.
One other tricky case is when the node to remove is the root. The root may fall into any of the cases above, but it doesn't have a parent! So that makes things more difficult. On way to get around this is to, when the remove method is invoked, create a new node to act as root's parent (rootParent)—assign root to rootParent's left child. Then perform the removal, and afterwards, set root to rootParent's left child and delete rootParent.
In order to remove a node, regardless of what case it falls into, we must first find it. This step follows closely to what we did for insertion, and is explained further when we cover the contains(item) operation.
Here's the pseudo code for this monster:
remove(item):
if root doesn't exist: return -- there's nothing to remove
make a node called rootParent with a dummy value
set rootParent's left child to root
removeHelper(item, root, rootParent)
removeHelper(item, node, parent):
if node contains the item:
check for case 1 -- node is a leaf:
remove the link to parent:
if node is parent's left child: set parent's left child to NULL
else: set parent's right child to NULL
delete the node
check for case 2 -- node has exactly one child:
let child be the child of node that exists
link node's parent to node's child:
if node is parent's left child: set parent's left child to child
else: set parent's right child to child
delete the node
check for case 3 -- node has both children:
let minNode be the smallest node in node's right subtree
let minNodeParent be minNode's parent
unlink minNode from minNodeParent (replace minNode with it's right
child, which may be NULL):
set minNodeParent's left child to minNode's right child
move minNode to node's position:
link parent to minNode:
if node is parent's left child:
set parent's left child to minNode
else:
set parent's right child to minNode
link minNode to node's children, as long as minNode is not
node's child:
if node's left child is not minNode:
set minNode's left child to node's left child
if node's right child is not minNode:
set minNode's right child to node's right child
delete node
else if item < node's data and node's left child exists:
removeHelper(item, node's left child, node)
else if item > node's data and node's right child exists:
removeHelper(item, node's right child, node)
contains(item)
The contains(item) method takes an item and returns whether or not it is contained within the tree. Again, we will use a recursive solution and it will mirror parts of the insert(item) and remove(item) methods. Basically, at each node, we consider whether it holds the item (e.g., the item equals the node's value); if so, we've located the item. Otherwise, if the item is less than the value stored in the node, we search the left subtree for it, or, if the left child doesn't exists, we know item is not the tree. If the item is greater than the node's value, we search the right subtree for it, or, if the right child doesn't exist, we know item is not th tree. Here's the pseudo code:
contains(item):
if root doesn't exist:
return false
return containsHelper(item, root)
containsHelper(item, node):
if item equals node's value:
return true
else if item < node's value and node's left child exists:
return containsHelper(item, node's left child)
else if item > node's value and node's right child exists:
return containsHelper(item, node's right child)
else
return false
[in,pre,post]OrderTraverse(function)
These three methods traverse the tree in a pre-order, in-order, or post-order fashion and, at each node, invokes function() on the node. The function can be anything—it might print the node's data out or it might check to see if the data is odd or even. It doesn't matter. Here's the pseudo code for each:
preOrderTraverse(function):
if root: preOrderTraverseHelper(function, root)
preOrderTraverseHelper(function, node):
function(node)
if node's left child exists:
preOrderTraversalHelper(function, node's left child)
if node's right child exists:
preOrderTraversalHelper(function, node's right child)
inOrderTraverse(function):
if root: inOrderTraverseHelper(function, root)
inOrderTraverseHelper(function, node):
if node's left child exists:
inOrderTraversalHelper(function, node's left child)
function(node)
if node's right child exists:
inOrderTraversalHelper(function, node's right child)
postOrderTraverse(function):
if root: postOrderTraverseHelper(function, root)
postOrderTraverseHelper(function, node):
if node's left child exists:
postOrderTraversalHelper(function, node's left child)
if node's right child exists:
postOrderTraversalHelper(function, node's right child)
function(node)
(Back to top)
Complexity and Balanced BSTs
In a BST implemented using the pseudo code above, operations have low average complexity, but in the worst case, are pretty bad. It all depends on how the tree has grown with inserts and removals. The maximum number of steps required to find a node (which we need for insert(item), remove(item), and contains(item))is the longest possible path within the BST, which is exactly the height of the tree. So whether our complexity is high or low depends on the height of the tree.
In the optimal case, a BST is balanced—roughly meaning that the left and right subtrees have almost equal heights and are filled out similarly. Here is an example of a balanced BST:
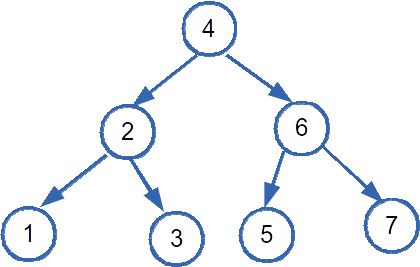
If a BST with size n is balanced, then the height is log2 n. Why? because the tree has a branching factor of two, then at each node, we are dividing the subtree rooted at it by two. The expression log2 n tells us how many times we can divide a set of n things in two. Therefore, the longest path in a balanced BST is log2 n, making the complexity O(log2 n).
The thing is, the exactly optimal case is unusual. A near optimal case is less unusual, but it day to day operations, the worst case is quite possible. What is the worst case? When the tree degenerates into a linked list. This happens when items are added in order or reverse order. For example, when adding the set {1,2,3,4,5,6,7}, the first item becomes the root, then each subsequent number is added as the right child of the previously inserted item. Then, the height of the tree becomes n because each node has one child, and therefore each level has one child. The complexity becomes O(n). Here's an example of a degenerate BST:
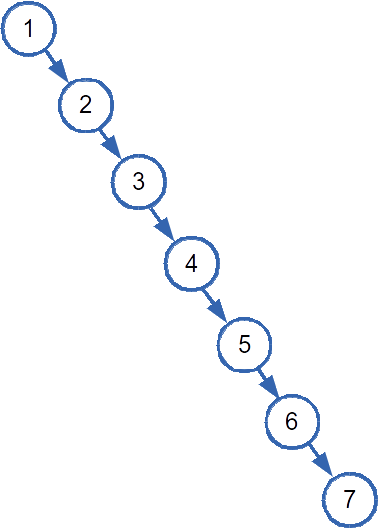
There are variants of trees called self-balancing trees. Depending on the algorithm, self-balancing trees will re-organize the tree so that it becomes more or less balanced, which helps eliminate the worst case performance. One issue is that re-balancing a tree is itself a costly operation, and so like most things in computing, there is a trade off.
(Back to top)